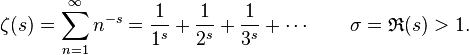→ June 15, 2015
→ By

The Golden Ticket.

Lance Fortnow wrote a piece for Communications of the Association for Computing Machinery in 2009 on the state of the P vs NP problem, one of the most important unsolved problems in both mathematics and computer science. That article led to the short (~175 page) book The Golden Ticket: P, NP, and the Search for the Impossible, which I recently read in its Kindle edition (it’s also on iBooks); Fortnow does a solid job of making an abstruse problem accessible to a wider audience, even engaging in some flights of fancy describing a world in which P equals NP … which is almost certainly not true (but we haven’t proven that yet either!).

P vs NP, which was first posed by Kurt Gödel in 1956, is one of the seven Millennium Problems posed by the Clay Mathematics Institute in 2000; solve one and you get a million bucks. One of them, proving the Poincaré Conjecture (which relates to the shape of the universe), was solved in 2010. But if you solve P vs NP affirmatively, you can probably solve the remaining five and collect a cool $6 million for your problems. You’ll find a box of materials under your desk.

Of course, this is far from an easy question to solve. P and NP are two classes of problems in computer science, and while it seems probable that they are not equivalent, no one’s been able to prove that yet. P is the set of all problems that can be quickly (in deterministic polynomial time – so, like, before the heat death of the universe) solved by an efficient algorithm; NP is the set of all problems whose solutions, once found, can be quickly verified by an efficient algorithm. For example, factoring a huge composite number is in NP: There is no known efficient algorithm to factor a large number, but once we’ve found two factors, a computer can quickly verify that the solution is correct. The “traveling salesman problem” is also in NP; it’s considered NP-complete, meaning that it is in NP and in NP-hard, the set of all problems which are at least as hard as the hardest problems in NP. We can find good solutions to many NP-hard problems using heuristics, but we do not have efficient algorithms to find the optimal solution to such a problem.

If P does in fact equal NP, then we can find efficient algorithms for all problems in NP, even those problems that are NP-complete, and Fortnow details all of these consequences, both positive and negative. One major negative consequence, and one in which Fortnow spends a significant amount of time, would be the effective death of most current systems of cryptography, including public-key cryptography and one-way hashing functions. (In fact, the existence of one-way functions as a mathematical truth is still an unsolved problem; if they exist, then P does not equal NP.) But the positive consequences are rather enormous; Fortnow gives numerous examples, the most striking one is the potential for quickly developing individualized medicines to treat cancer and other diseases where protein structure prediction is an obstacle in quickly crafting effective treatments. He also works in a baseball story, where the game has been dramatically changed across the board by the discovery that P=NP – from better scheduling to accurate ball/strike calls (but only in the minors) to the 2022 prohibition of the use of computers in the dugout. It’s Shangri-La territory, but serves to underscore the value of an affirmative proof: If we can solve NP problems in deterministic polynomial time (as opposed to nondeterministic polynomial time, where NP gets its name), our ability to tease relationships out of huge databases and find solutions to seemingly intractable logical and mathematical problems is far greater than we realized.

Of course, P probably doesn’t equal NP, because that would just be too easy. That doesn’t mean that NP-complete problems are lost causes, but that those who work in those areas – operations research, medicine, cryptography, and so on – have to use other methods to find solutions that are merely good rather than optimal. Those methods include using heuristics that simplify the problem, approximating solutions, and solving a different but related problem that’s in P. If Fortnow falls short at all in this book, it’s in devoting so much more time to the brigadoon where P=NP and less to the likely real world quandary of solving NP-complete problems in a universe where P≠NP. He also gives over a chapter to the still theoretical promise of quantum computing, including its applications to cryptography (significant) and teleportation (come on), but it seems like a digression from the core question in The Golden Ticket. We don’t know if P equals NP, but as Fortnow reiterates in the conclusion, even thinking about the question and possible approaches to proving it in either direction affect work in various fields that underpin most of our current technological infrastructure. If you’ve ever bought anything online, or even logged into web-based email, you’ve used a bit of technology that only works because, as of right now, we can’t prove that P=NP. For a very fundamental question, the P vs NP problem is scarcely known, and Fortnow does a strong job of presenting it in a way that many more readers can understand it.

If this sounds like it’s up your alley or you’ve already read it, I also suggest John Derbyshire’s Prime Obsession, about the Riemann Hypothesis, another of the Clay Millennium Institute’s six as-yet unsolved problems.

Filed Under: Uncategorized Tagged With: , , , ,
→ June 11, 2015
→ By

Proofiness.

Whew! I’m glad that’s over. For Insiders, my recaps of the drafts for all 15 NL teams and all 15 AL teams are up, as well as my round one reactions and a post-draft Klawchat.

Charles Seife’s Proofiness: How You’re Being Fooled by the Numbers is a beautiful polemic straight from the headquarters of the Statistical Abuse Department. Seife, whose Zero is an enjoyable, accessible story of the development and controversy of that number and concept, aims both barrels at journalists, politicians, and demagogues who misinterpret or misuse statistics, knowing that if you attach a number to something, people are more inclined to believe it.

Seife opens with Senator Joseph McCarthy’s famous claim about knowing the names of “205 … members of the Communist Party” who were at that moment working in the State Department. It was bullshit; the number kept changing, up and down, every time he gave a version of the speech, but by putting a specific number on it, the audience assumed he had those specific names. It’s a basic logical error: if he has the list of names, he must have the number, but that doesn’t mean the converse is true. He rips through a series of similarly well-known examples of public abuse of statistics, from the miscounting of the Million Man March to stories about blondes becoming extinct to Al Gore cherrypicking data in An Inconvenient Truth, to illustrate some of the different ways people with agendas can and will manipulate you with stats.

One of the best passages, and probably most relevant to us as the Presidential election cycle is beginning, is on polls – particularly on how they’re reported. Seife argues, with some evidence, that many reporters don’t understand what the margin of error means. (This subject also got some time in Ian Ayers’ Super Crunchers, a somewhat dated look at the rise of Big Data in decision-making that has since been lapped by the very topic it attempted to cover.) If done correctly, the margin of error should equal two standard deviations, but many journalists and pundits treat it as some ambiguous measure of the confidence in the reported means. When Smith is leading Jones 51% to 49% with a margin of error of ±3%, that’s not a “statistical dead heat;” that’s telling you that the poll, if run properly, says there’s a 95% chance that Smith’s actual support is between 48% and 54% and a 95% that Jones’ support is between 46% and 52%, with each distribution centered on the means (51% and 49%) that were the actual results of the poll. That’s far from a dead heat, as long as the poll itself didn’t suffer from any systemic bias, as in the famous Literary Digest poll for the 1936 Presidential election.

Seife shifts gears in the second half of the book from journalists to politicians and jurists who either misuse stats for propaganda purposes or who misuse them when crafting bad laws or making bad rulings. He explains gerrymandering, pointing out that this is an easy problem to solve with modern technology if politicians had any actual interest in solving it, and breaks down the 2000 Presidential vote in Florida and the 2008 Minnesota Senate race to show that the inevitable lack of precision even in popular votes and census-taking mean both races were, in fact, dead heats. (Specifically, he says that it is impossible to say with any confidence that either candidate was the winner.) Seife shows how bad data have skewed major court decisions, and how McCleskey v. Kemp ignored compelling data on the skewed implementation of capital punishment. (Antonin Scalia voted with the majority, part of a long pattern of ignoring data that don’t support his views, according to Seife.) This statistical abuse cuts both ways, as he gives examples of both prosecutors and defense attorneys playing dirty with numbers to claim that a defendant is guilty or innocent.

For my purposes, it’s a good reminder that numbers can be illustrative but also misleading, especially since the line between giving stats for descriptive reasons can bleed into the appearance of a predictive argument. I pointed out the other day on Twitter that both Michael Conforto and Kyle Schwarber were on short but impressive power streaks; neither run meant anything given how short they were, but I thought they were fun to see and spoke to how both players are elite offensive prospects. (By the way, Dominic Smith is hitting .353/.390/.569 in his last 29 games, and has reached base in 21 straight games!) But I’d recommend this book to anyone working in the media, especially in the political arena, as a manual for how not to use statistics or to believe the ones that are handed to you. It’s also a great guide for how to be a more educated voter, consumer, and reader, so when climate change deniers claim the earth hasn’t warmed for sixteen years, you’ll be ready to spot and ignore it.

Next up: I’m way behind on reviews, but right now I’m halfway through Adam Rogers’ Proof: The Science of Booze.

Filed Under: Uncategorized Tagged With: , , , , ,
→ June 3, 2015
→ By

Incompleteness.

My final top 100 draft prospect ranking for 2015 is up for Insiders, and my latest review for Paste covers the Temple of Elemental Evil boardgame.

Rebecca Goldstein’s Incompleteness: The Proof and Paradox of Kurt Gödel, part of the same “Great Discoveries” series that includes David Foster Wallace’s Everything and More: A Compact History of Infinity, takes the abstruse topic of Gödel’s two incompleteness theorems and folds it into a readable, compelling biography of both the man and his ideas. Using the logician’s friendship with Albert Einstein as a hook, Goldstein gives us about as intimate a portrait of the intensely private Gödel as we can get, while also laying the groundwork so the non-metamathematicians among us can understand the why and how of Gödel’s theorems.

There’s very little actual math involved in Incompleteness, because the two theorems in question revolve around the nature of mathematics, notably arithmetic, as an axiomatic system that mathematicians and philosophers of the early 1900s were trying to use as a basis to describe arithmetic as a formal system – that is, one that can be fully described via a system of symbols and syntax, used to construct well-formed formulas (wffs, not to be confused with wtfs), some of which are the axioms that define the whole system. If such axioms can describe the entire system in a way that an algorithm (which is probably easiest to conceive as a computer program) can use those axioms and only those axioms to prove all truths or assertions about the natural numbers, then arithmetic would be considered a complete system, something Gödel proved was impossible in his first theorem. His second theorem went even further, showing that such a system of arithmetic also could not be consistent within itself by demonstrating that a statement of the system’s consistency would generate an internal contradiction.

Gödel imself was an incomplete figure, a hypochondriac who degenerated into outright paranoia later in life, and a socially awkward man who would likely have been diagnosed in today’s world of psychiatry and medicine as a depressive or even somewhere on the autism spectrum. He formed few lasting friendships, feared that no one could understand him (and given the meandering paths of his mind, I don’t doubt this was true), and was often shockingly aloof to what was happening around him. He fled his native Austria before World War II, even though he wasn’t Jewish, because his association with the secular Jewish scholars of the Vienna Circle (most of whom were logical Positivists, arguing that anything that could not be empirically proven could not be considered true) cost him his university position. Yet he remained unaware of the state of affairs in his native country, once (according to Goldstein) asking a Jewish emigré who had fled Nazi persecution for the United States, “What brings you to America?”

Goldstein does a superb job setting the scene for Gödel’s emergence as a logician/metamathematician and as a figure of adulation and controversy. The Vienna Circle was, in Goldstein’s depiction, somewhat insular in its unwavering acceptance of Positivism, and as such certain that Hilbert’s second problem, asking for a proof that arithmetic is internally consistent, would be proven true. Gödel’s second theorem showed this was not the case, leading to his own intellectual isolation from thinkers who were heavily invested in the Positivist view of mathematics, a bad outcome for a man who was already prone to introversion and diffidence. G&omul;del found it difficult to express himself without the use of logic, and while his station at Princeton’s illustrious Institute for Advanced Study – a sort of magnet think tank that became a home for great scholars in math and the sciences – put him in contact with Albert Einstein, it also deepened his solitude by limiting his orbit … although that may have been inevitable given his late-life delusions of persecution. Goldstein did encounter Gödel once at a garden party at Princeton, only to see him at his most gregarious, holding court with a small group of awestruck graduate students, only to disappear without a trace when his spell of socializing was over. He was, in her description, a phantom presence around campus, especially once his daily walks with Einstein ended with the latter’s death in 1955.

While giving a basic description of Gödel’s theorems and proofs, focusing more on their implications than on the underlying math, Goldstein does send readers to the 1958 Gödel’s Proof, a 160-page book that attempts to give readers a more thorough understanding of the two theorems even if those readers lack any background in higher math. Incompleteness focuses instead on the man as much as it does on his work, producing a true narrative in a story that wouldn’t otherwise have had one, making it a book that I could recommend to anyone who can stand Goldstein’s occasional use of a $2 word (“veridical”) when a ten-cent one (“truthful”) would have done.

Filed Under: Uncategorized Tagged With: , , , ,
→ March 21, 2015
→ By

Saturday five, 3/21/15.

My ESPN Insider content from the last week:

* My breakout player picks for 2015.
* A suggested rule change to cover the Kris Byrant situation, plus Jonathan Gray, Tyler Matzek, Yasmany Tomas, and Yoan Lopez
* Javier Baez, Brandon Finnegan, Danny Duffy, Kyle Schwarber
* Carlos Rodon and Tyler Danish
* Taijuan Walker and Rubby de la Rosa
* A draft blog post on Arizona infielders Kevin Newman and Scott Kingery

I’ll be on the ESPN game broadcasts on Tuesday (Phillies at Atlanta) and Friday (Red Sox at Atlanta), as well as some postgame content to be determined.

And now, this week’s links…

  • There’s been a rash of suicides and attempts in Palo Alto, prompting this sound and accessible piece on how parents can try to help decrease the risks in their own children.
  • This week in terrifying food science news: Antibiotic use at pork farms is soaring, and it’s not just in the United States. Of course, we can’t expect other countries to ban the practice if we refuse to do it ourselves.
  • A Virginia middle school suspended a sixth-grader and referred him for substance-abuse counseling because he brought a leaf to school. No, not a marijuana leaf, or any other kind of illicit drug. This is zero-tolerance policy run completely amok, benefiting no one.
  • It’s made the rounds, but just in case you haven’t seen it, Ashley Judd is seriously sick of your misogynistic bullshit. Death threats are illegal, so why aren’t rape threats? More importantly, why does Twitter persistently refuse to do anything about it?
  • Making busy intersections safer. I imagine the initial reluctance to accept these new designs would be huge – never change anything, anywhere – but they’re fascinating to me as someone who used to love road maps and seeing different streets and intersections as a kid, but also to me as someone who drives all the time and worries a lot about getting in or even causing an accident. Although the skateboarder I nearly brained on San Diego Avenue on Thursday shouldn’t have been in the middle of the car lane, even at midnight.
  • “Hands up, don’t shoot” was built on a lie. Or maybe it wasn’t. Hell if I know.
  • Finally, Baltimore Ravens lineman John Urschel co-authored a math paper titled “A Cascadic Multigrid Algorithm for Computing the Fiedler Vector.” Are we praising him for being brilliant, or are we all just relieved that he’s not a wife-beater or a serial rapist? Regardless, graph theory is heady stuff, beyond anything I ever studied in school or on my own; I remember encountering the Königsberg Bridge Problem, a precursor to modern graph theory, but don’t recall learning its (dis)proof.
Filed Under: Uncategorized Tagged With: , , ,
→ March 13, 2015
→ By

Two math anthologies.

My latest Insider post covered scouting notes on Danny Salazar, Kendall Graveman, and others from that same game. My weekly Klawchat transcript is up, and I have a new boardgame review over at Paste for the Kennerspiel des Jahres-nominated strategy game Rococo.

My friend Steve is quite familiar with my affinity for just about all things math – we first met in math class in seventh grade – and for Christmas this year bought me a pair of popular math texts, one new and one classic. (I bought him a lot of tea, as he consumes it even faster than I do.) Both were collections of short pieces, with the unevenness that comes with such an anthology, but with high points making both books well worth reading.

The new title was The Best Writing on Mathematics 2014, a book that opens with a sort of dry exhortation on the apparently declining interest in math among students, a theme revisited later in the book, although I think a large part of that is a function of how we teach math in the United States – something that is in and of itself the subject of a separate essay. The separation of abstract math from its practical uses will only sit well with students who are naturally able to deal with math’s abstractions, to hear the music in numbers and formulas, to understand topics like calculus on an intuitive level; modern American instruction tends to make the majority of students, those who don’t grasp this material as quickly, feel less able or competent in the subject. Math anxiety, the subject of so-and-so’s column, isn’t an innate medical condition like anxiety disorder; it is created by teachers and curricula that quickly tell students they’re just not good enough at this stuff.

I enjoy abstract math – one of the best books I’ve ever read was on the highly abstruse Riemann Hypothesis, called Prime Obsession, one of the great unsolved problems in mathematics and one without any apparent practical applications. Yet I also enjoy writing on the pervasive uses of math in other fields, from physics to probability. One of the best essays in the book, and unfortunately one of the shortest, is from game designer and engineer Soren Johnson, who discusses the uses of probability and controlled randomness in creating successful games, specifically citing the random component in Settlers of Catan that has diminished its standing among the most hardcore boardgaming segment that prefers the less random and more complex style of games like Puerto Rico or Agricola. (My issue with Settlers isn’t the randomness but the length of the games. It’s still a classic and one of the best light-strategy games ever created.)

There are several pieces built around randomness, including a high-level essay from Charles Seife (author of Zero, which I enjoyed, as well as Proofiness: How You’re Being Fooled by the Numbers, which is on my to-be-read shelf) on the nature of randomness and our inability to understand it, and another essay on the power of the random in musical compositions. The essay by Prakash Gorrochum titled “Errors of Probability in Historical Context” should be required reading for journalists everywhere, covering the gambler’s fallacy, reasoning on the mean, and misunderstanding statistical independence (Bayes’ theorem). One essay tackles the problem of the Jordan Curve – defined a simple closed curve in a plane or planar region, dividing it into exactly two parts, thus never crossing itself – and its applicability to some amazing works of art. I alluded to the closing essay on Twitter the other day; it discusses the proposed solution to the abc problem, for which the alleged solver had to invent a whole new kind of mathematics, which means that only a few dozen people in the world might be able to interpret his proof, let alone test or critique it.

The selection of titles seems idiosyncratic, as some have very little to do with math proper, such as the dreadful essay on various ancient tools and devices used for mathematical calculations, or the too-lengthy chapter disproving the contention that ancient Celts in modern-day Scotland knew and understood the features of the five regular polyhedra a millennium before anyone else seemed to catch on. The collection ends on several high notes, however, including Gorrochum’s essay (which you can read in its entirety online) and that abc problem/solution story, the latter of which is almost creepy because of how bizarre the whole backstory is. I’d never heard of this series before Steve bought me this book but the handful of strong essays in it made it a great read.

—

The other book Steve bought for me was Martin Gardner’s collection Hexaflexagons, Probability Paradoxes, and the Tower of Hanoi, which is the first in the series of books anthologizing Gardner’s many essays on popular math from his long-running column in Scientific American. Gardner’s writing exudes his sheer joy in math itself, yet most of these essays explore tangible questions even when they’re as useless as the hexaflexagons of the book’s title. Those peculiar shapes are formed by folding one or more strips of paper according to prescribed patterns to form regular polygons, in this specific case hexagons, that can be pushed and folded to reveal hidden sides and features, a chance discovery explored by some very famous names from math and science (Richard Feynman was among their earliest practicioners). A similar vein runs through his essays on the games Hex, invented independently by Nobel Prize-winning game theorist John Nash and Danish polymath Piet Hein, a totally nonrandom game of tile placement on a rhomboid board of hexagonal spaces where each player is trying to complete an unbroken chain from one of his sides to the side facing it. The game can’t end in a draw, and on smaller boards there are unbeatable strategies for whichever player goes first, inspiring much mathematical hand-wringing over the search for algorithms to predict perfect plays.

Other essays pose specific logic and math puzzles to the reader, many of which can be worked out in your head (and are much worse if you start putting pencil to paper). He explores the history of the “boss puzzle,” also known as the 15-14 puzzle, where the player is presented with a 4×4 grid with 15 numbered tiles on it, all in ordered rows but with the final row going 13-15-14. The player is told to use the single open space to move tiles around to get all fifteen tiles into the proper order. (The puzzle is unsolvable because it has a parity of one, meaning there’s a single tile displacement.) He also discusses several popular math and logic paradoxes, such as the division of a rectangle into several triangular pieces, then the reassembly that makes it appear that some surface area has disappeared. (It hasn’t.) They’re fun to puzzle over for their own sake, but the sleights of math used here or in the card tricks Gardner describes in another chapter expose holes in our critical thinking processes – ways we can miss obvious fallacies because something looks or sounds “right” on its face.

The chapter that might be most familiar to readers in subject matter discusses the Birthday Paradox. Given a group of 24 people selected at random, what are the odds that at least two members of the group have the same birthday? The answer is better than one half, which seems at first rather hard to believe as there are 365 days in the calendar. The odds that the first two people don’t have the same birthday are 364/365; the odds that the third person added to the group won’t have the same birthday as either of the first two are 363/365; and so on. The probability that n people won’t have the same birthday is thus a product of all of these individual probabilities (the formula is here); the 23rd person added to the group drops the probability that there is no birthday match under 0.5. It seems intuitively incorrect that just 23* people could suffice to raise the odds of a match over 50% when the number of dates is 365, and there are many methods of figuring these odds incorrectly, such as multiplying the apparent odds of a match (2/365 * 3/365 * 4/365…) or adding up the same fractions. Gardner’s explanations of such paradoxes were both clear and a pleasure to read, which is why so much of his work remains in print a half-century after he started writing. The chapter doesn’t discuss the Monty Hall problem, but describes a similar question around hands of cards that might illuminate that more famous question if you’ve struggled to understand its explanation.

* Gardner’s chapter uses 24 as the threshold, but I’m pretty sure it’s 23, using both methods to calculate the odds. If anyone can show the magic number is 24, please post it in the comments, because then I’ve got this wrong too.

Gardner also discusses magic squares, which seem to me to be the logical ancestors of the much simpler sudoku; the Tower of Hanoi problem; and some topological oddities that arise from manipulations of a Mobius strip (or two of them together). He gets a little ahead of himself, perhaps a function of the space limitations of the print world, in the chapter on fallacies by presenting two pure math fallacies without explaining exactly why they fail. Both revolve around attempts to prove that two unequal entities are equal; one fails through a disguised attempt to divide by zero, the other by treating i as a real (rather than imaginary) number, but I wouldn’t assume either fallacy was obvious by the way Gardner presents them.

I first encountered Gardner’s work in junior high school through his now out-of-print Aha! Gotcha! book, which took a similar approach to math tricks and paradoxes but was aimed at a younger audience; Hexaflexagons is the more grown-up version, aimed at math-loving kids like me who just refused to grow up.

Filed Under: Uncategorized Tagged With: ,
→ November 26, 2014
→ By

Everything and More: A Compact History of Infinity.

I knew David Foster Wallace was brilliant when I read Infinite Jest, a wildly imaginative, sprawling novel that showcased DFW’s prodigious vocabulary as well as his deep knowledge of a variety of seemingly unrelated subjects. Even with that background, I was flabbergasted by Everything and More: A Compact History of Infinity, in which DFW delves into abstract set theory and other similarly abstruse topics from the history of math, explaining much of it lucidly and with humor until he gets too close to the finish to avoid relying on the reader to understand more of set theory than most readers will.

The book is less an explanation of the number infinity – which isn’t a single number, at least not in the sense that 1 or 5 or π or √2 – than the history of mathematicians’ attempts to deal with it. DFW starts with the Greeks, where most math stories begin anyway, even though the Greeks didn’t like or accept infinity or zero or the irrationals. (Zero came from Indian mathematicians, and reached Europe by way of Arab mathematicians quite a bit later.) The Greeks encountered questions around infinity, particularly in the famous paradoxes of Zeno, who liked to play semantic games around what we now refer to as convergent series – a sum of a series of terms that never ends but that approaches a specific limit as the number of terms grows. (In a related note, DFW fails to answer the question of how Zeno never got punched in the face for coming up with these paradoxes.) This discomfort with infinity continued through the writings of Aristotle and the Catholic Church’s influence over all manner of academic research, which included the idea that infinity was the sole province of God rather than of man, meaning we never got anywhere with infinity until the end of the Dark Ages and the separation of mathematics and religion during the Renaissance.

The pace of the narrative picks up at that point thanks to the explosion of advances in math and related areas of science. The empirical foundation that limited mathematical explorations until the 1600s is tossed aside in favor of more abstract thinking, with appearances by Kepler, Newton, and my homeboy Galileo, as trigonometry and eventually calculus displace geometry as the central philosophy guiding mathematical thinking and what we now think of as number theory. DFW presents an extraordinarily clear explanation of calculus, especially the infitesimals that underpin differentiation and integration and, as the name implies, connect it to the main topic of the book. The goal here is to get to Georg Cantor, the brilliant and mentally ill mathematician whose work remains the foundation of modern set theory and who was the first to recognize that there are different degrees of infinity (ℵ0 and ℵ1, at the least) but died unable to prove that those two infinities had no other infinities between them.

DFW’s writing is clear and witty thoughout the book, with many examples drawn from a former professor of his that help elucidate many of the more recondite concepts around infinity. His explanations of one-to-one mapping and Cantor’s diagonalization method of proving that real numbers are nondenumerable are outstanding, especially the latter, which I knew was true but still wanted to disbelieve because it just sounds impossible. Unfortunately, in the last 40-50 pages of the book, DFW gets so far down the set theory rabbit-hole that I found it increasingly hard to follow, such as discussions of ordinality versus cardinality and power sets of power sets. I got off the math train in college after multivariate calculus with vectors, in part because continuing meant pushing into more abstract areas – linear algebra was the next course, which starts the shift from empirical math to abstract – but that left me a little lost as Everything and More slid into Cantor’s work on the various infinities and work on numerability of sets.

Cantor’s transfinite numbers are the real goal of the narrative here, rather than what I would call the lay opinion of ∞ (what Cantor referred to as “absolute infinity”). A transfinite number is infinite in that it is greater than all of the finite numbers, but has some properties in common with the finites. If you’re familiar with the ℵ0 I mentioned above – the first transfinite cardinal number, corresponding to the number of members (cardinality) of the set of natural numbers (non-negative integers). Cantor’s continuum hypothesis, which appeared first on the famous list of unsolved math problems David Hilbert presented in 1900, posited that there was no set with cardinality (number of members) between the natural numbers and the real numbers (the cardinality of which Cantor designated as ℵ1). The hypothesis itself may be unprovable, at least within the confines of Zermelo-Fraenkel set theory … which DFW mentions but doesn’t explain, concluding instead with the explanation that later work by Kurt Gödel (the incompleteness guy) and Paul Cohen (who proved that the hypothesis and the ZFC’s axiom of choice were independent) set the question aside without really solving it. At least, I think that’s what he said, because I was just barely treading water by the final page. Which also made me wonder if all of these reviewers quoted as giving the book raves actually finished and understood the whole thing; I imagine the number of people who have sufficient math background to follow DFW down to the bitter end is pretty small.

Apropos of nothing else, the biggest laugh I got from the book was when DFW referred to a mathematician as a world-class pleonast, which is the pot writing a three-page letter to the editor about the mote in the kettle’s eye.

Next up: Ned Beauman’s 2012 novel The Teleportation Accident, recommended by a fellow bibliophile I met in New York in August.

Filed Under: Uncategorized Tagged With: , ,
→ July 9, 2014
→ By

The Solitude of Prime Numbers.

The Italian physicist Paolo Giordano became the youngest winner ever of the Premio Strega, Italy’s equivalent to the Pulitzer Prize for Fiction, when his debut novel, The Solitude of Prime Numbers, took the award in 2008. It became a feature film in Italian in 2010 and made its way here in an English translation that same year, earning very positive reviews around the world for its prose and the development of its two central characters. It is a beautiful rendering of those two horribly broken individuals, and one of the saddest novels I have ever read.

Giordano begins the novel by breaking those two characters in harsh, haunting ways. Alice, pushed too hard by a father whose impetus is never quite clear, suffers a horrible accident while skiing that leaves her scarred, disabled, and bitter. Mattia, meanwhile, is saddled with a twin sister who is severely developmentally disabled, and one day, while taking her to a birthday party to which they’ve both been invited, he leaves her in a park and tells her to wait there for him rather than taking her to the party. She vanishes and is never seen again, leaving Mattia a shell who fears the outside world and inflicts compensatory punishment via self-mutilation.

Solitude cover The two end up meeting in secondary school and forge a friendship based on their mutual recognition of each other’s willful isolation. Mattia is a math genius who has a single friend, Denis, who himself is gay and in love with Mattia but, of course, closeted and himself ostracized from the cruel society of his classmates. Those same classmates taunt or ignore Alice, and eventually the school’s mean girls clique targets her, both because of her disability and her late entry into puberty – the result of her anorexia, which worsens as she gets older. Mattia and Alice seem like a perfect couple, the two peas in the pod on the paperback’s cover, but Giordano argues through his prose that people this detached from others cannot be together. They are twin primes: Two prime numbers with a difference of two, like 11 and 13 or 59 and 61, as close as a pair of odd primes can get, but never actually adjacent. (Only 2 and 3 are neighboring primes. Because 2 is the only even prime, all other pairs must be separated by at least two places on the integer scale.)

Eventually, other circumstances drive Mattia and Alice apart, both as a couple and as neighbors, as Mattia takes a job in Germany and Alice ends up in another relationship. But a strange coincidence, one that Giordano wisely never confirms in full, brings them back together for one final attempt at … something, a connection if not an actual romance, because Giordano hasn’t given us any reason to believe these two broken people can heal themselves enough to be with each other. If this were Hollywood, they’d promise to fix each other (with Coldplay softly playing in the background) and that would be the ending. Giordano gives us ambiguous realism rather than pat endings, and while it doesn’t offer the catharsis a book this sad might call for, it keeps the ending in tune with the remainder of the story.

Alice’s character felt more familiar than Mattia’s, probably because we’ve all known someone who had one of her major issues – a physical disability, leading to social isolation; or an eating disorder. Piling both on Alice might have made her more pathetic, yet Giordano gave her more strength of character, more forcefulness than Mattia, to balance the scales. Mattia’s disappearance into math, especially into research on prime numbers (and specifically Riemann’s zeta function, a key component in the search for a proof or disproof of the Riemann Hypothesis, an unsolved problem detailed extremely well in the book Prime Obsession), further underscores his difficulty with communication – as if a man that comfortable with numbers and order could ever be comfortable in the subjective, anarchic world of words and feelings. He comforts himself by counting objects or looking for familiar shapes or structures in the world, but eventually ends up hurting himself or drawing his own blood in almost every disturbing situation. Is it really right to expect two “primes,” two loners whose self-inflicted solitude has become inescapable, to be able to save each other when neither is capable of helping him- or herself?

As gorgeous as Giordano’s rendering of his characters, even secondary ones like Denis or Alice’s housekeeper Soledad, can be, Solitude can also be intensely painful to read because of the damage he inflicts on them, as if he were pushing and prodding them to see how far they can bend without breaking. Where Alice responds with anger, Mattia responds by becoming increasingly insular, as if even the solitude he finds in numbers isn’t alone enough for him. I was also a little surprised that none of Mattia’s or Alice’s parents seemed to take an active role in trying to draw their children out, showing more resignation, perhaps provoked by guilt (on Alice’s father’s side) or shame (for Mattia’s parents). The only hints of this come with the primes’ rejection of their parents as adults, something I found even more painful now as a parent – to love and raise a child, only to find that child has no use for use once she’s grown, would be the dementor’s kiss of parenthood.

If you’ve already read Solitude, Giordano’s second novel, The Human Body, will be released in the U.S. on October 2nd.

Next up: J.K. Rowling’s first non-Potter novel, The Casual Vacancy.

Filed Under: Uncategorized Tagged With: , ,
→ January 25, 2014
→ By

The Man Who Knew Infinity.

Ramanujan was one of the most remarkable and prolific mathematicians who ever lived, a self-taught prodigy who grew up in modest circumstances in south India during the time of the British Raj, rediscovering the previous 150 years’ worth of number theory while also uncovering over 3000 theorems and identities of his own. “Discovered,” in a sense, by the far more famous English mathematician G.H. Hardy, Ramanujan moved to England for about five years, where his work finally received a wider audience, but where he also contracted an unknown illness that eventually killed him at age 38.

Robert Kanigel’s biography The Man Who Knew Infinity: A Life of the Genius Ramanujan tells two main stories – that of Ramanujan himself, and a partial biography of Hardy, whose professional life was thoroughly altered by his time working with Ramanujan and to whom we owe most of the credit for what we know of Ramanujan’s life and work today. It’s a very strong, even-handed biography of Ramanujan, sympathetic without becoming patronizing, but was extremely light on its discussion of the math itself, with just a few cursory discussions of some of his findings that still bear his name today.

Born in southern India in what is now the state of Tamil Nadu, near the city of Madras (now known as Chennai), Ramanujan was a member of the Brahmin caste, the highest social stratum in the caste system, but was born into a poor family and received only a basic education. His mother was domineering and remained deeply involved in his life even into his adulthood and arranged (by her) marriage, only, according to Kanigel, supporting her son’s obsession with mathematics when it appeared it would at least bring him fame – and bring her fortune. Ramanujan failed out of university twice because he couldn’t be bothered with any coursework other than mathematics, but in that subject he was light-years ahead of his professors, filling notebooks with conjectures and equations, most of which he knew intuitively to be true, but couldn’t have published – even if he’d had access to such outlets – because he didn’t need to or understand how to develop the proofs.

In 1912 and 1913, Ramanujan, at the encouragement of some of the few Indian nationals in a position to advise him, sent letters with copies of some of his work to three English mathematicians, only one of whom responded: G.H. Hardy, at the time a professor of maths at Trinity University at Cambridge. Hardy was a purist, a mathematician who studied number theory (the study of the behavior and properties of the integers, with a special emphasis on prime numbers) for its own sake and overtly disdained any branch of “applied” mathematics – that is, math that had a practical purpose, such as the math required in physics or engineering. Hardy was open-minded enough upon seeing Ramanujan’s letter that he overcame his skepticism about an uneducated Indian clerk coming up with mathematical insights that took Western experts over a century to develop and wrote back, asking to see more of Ramanujan’s work. (There’s some irony in Hardy’s hesitation and the other mathematicians’ rejections of Ramanujan, as number theory has its own tradition in India dating back over 1500 years.) The subsequent correspondence led to an invitation for Ramanujan to come spend two years with Hardy at Cambridge, two years that turned into five before ill health sent Ramanujan back home to south India, where he died shortly thereafter.

Kanigel’s presentation of the life of Ramanujan leans toward the personal rather than the professional side, focusing extensively on his upbringing, cultural opposition to much of what he did and wanted to do with his life, and on the non-professional side of his life in England. The emotional cost to Ramanujan of traveling to a foreign country where he’d face outright prejudice but also would struggle with differences in language, weather, and, most importantly for Ramanujan, food. The devoutly spiritual and nominally Hindu mathematician was a strict vegetarian, but had great difficulty adapting his diet to the abysmal food of World War I-era England, where to cook something implied cooking it to death, where all flavor and texture was safely removed from the item to be consumed. Hardy was Ramanujan’s mentor in maths, but not in life, as Hardy does not (in Kanigel’s telling) have any close emotional ties to anyone but his sister once their parents had passed away, and with Ramanujan’s wife in India for the entire time he was in England, Ramanujan lacked for friends and for anyone who could help him look after himself. Kanigel reports on the speculation that malnutrition contributed to Ramanujan’s illness and decline, but his book was published before the 1994 report that he died of an amoebic infection in his liver common in India at the time he lived there.

I also found Kanigel’s mini-biography of Hardy, essential to the story of Ramanujan, fascinating. Hardy’s a great figure for biographers, appearing in one of my favorite books about math, Prime Obsession, for his role in attacking the unsolved Riemann Hypothesis. (Ramanujan’s pre-Hardy work was remarkable, but he did make some mistakes, one of which involved Riemann’s zeta function; Ramanujan assumed the function had only real zeroes, not complex ones, but its complex zeroes lie at the heart of the Hypothesis.) He’s also ripe for caricature, something Kanigel avoids entirely. A lifelong bachelor, Hardy was obsessed by numbers, but also had an equal passion for cricket (and, after a stint at Princeton, baseball). He was a strict atheist who once set out a goal for himself to craft a disproof of the existence of God convincing enough to convert most of the general public, and a pacifist who fought persecution of Trinity colleagues who spoke out against British involvement in World War I. Hardy viewed Ramanujan with great pride, almost as a father would view a son, someone with limitless natural talent whom Hardy could mold into one of the greatest mathematicians the world has ever known, and he was diligent about assigning credit to his protégé whenever possible. He brought Ramanujan to the world, yet it also seems that Ramanujan brought much more out of Hardy than we’d otherwise have had.

My lone criticism of The Man Who Knew Infinity is its scant treatment of the math in question. The reader of a book like this probably has an appetite for math, and the author has merely to explain the theorems or identities under discussion, not to teach them or prove them. Kanigel does very little of any of this, only dipping occasionally into discussions of continued fractions and some of Ramanujan’s explorations of the nature and frequency of prime numbers. Kanigel appears to have skipped the mathier material in favor of asking open-ended questions about the source of Ramanujan’s inspiration and culpability for his illness and death.

Kanigel’s epilogue discusses the final years of Hardy’s life, but it is his discussions with Ramanujan’s widow, Janakiammal, that punctuate the book’s last handful of pages. Still alive at the time of the book’s publication in 1991, Janakiammal spent a long part of her life as a widow in obscurity and poverty before she was rediscovered several decades after her husband’s passing, eventually reaping rewards, both honorary and monetary, before her death in 1994 at age 95. Her few comments evoke a great bitterness at how her husband’s legacy was underappreciated and how her own life was adversely affected by that and by quarrels with Ramanujan’s family.

Next up: The Supper of the Lamb: A Culinary Reflection (Modern Library Paperbacks) by Robert Farrar Capon, a chef and Episcopalian priest. The 1967 book is a classic of the food-writing genre and was reissued in 2002 as part of the Modern Library Food series, edited by Ruth Reichl.

Filed Under: Uncategorized Tagged With: , , ,
→ July 23, 2012
→ By

The Golden Ratio.

Some recent ESPN links: Analyses of the Jays/Astros ten-player trade and the Brett Myers trade, as well as a big post on players I’ve scouted in the AZL over the last week, including Jorge Soler. The Conversation under the Myers piece has been rather bizarre, as a few (presumably male) readers are saying I shouldn’t have brought up Myers’ 2006 arrest on domestic violence charges. Needless to say, I think these complaints are spurious.

—

I’m a big fan of mainstream books about mathematics, most of which would probably be best classified as “history of math” even if they’re discussing a currently unsolved problem, such as John Derbyshire’s excellent book on the Riemann Hypothesis, Prime Obsession. (And yes, I’m aware of Derbyshire’s political writing, but that doesn’t change the fact that the Riemann book is very well done.) Mario Livio’s book The Golden Ratio: The Story of φ, the World’s Most Astonishing Number was on my wish list for a long time because it seemed like a perfect blend of the academic and applied branches of mathematics, as the irrational number φ appears in numerous places in nature and (I thought) art. Unfortunately, Livio’s book spends more time talking about where φ is not than about where it is, making this more of a book of mythbusting than of math.

Livio does provide a solid introduction to φ, an irrational number equal to (1 + √5)/2 = 1.6180339887… that has several interesting properties, including:

* φ2 is equal to φ + 1, or 2.6180339887…
* 1/φ is equal to φ – 1, or 0.6180339887…
* If you take any line segment AB and place a point C on it such that the ratio of the longer half to the shorter half is equal to the ratio of the entire segment to the longer half, the ratio in question will be equal to φ
* The ratio between consecutive terms in the Fibonacci sequence – the series 0, 1, 1, 2, where each successive term is equal to the sum of the two terms before it, thus continuing with 3, 5, 8, 13, 21, ad infinitum – approaches φ. The ratio between the 17th and 16th terms is already 1.61800328…
* φ is also the result of the peculiar expression

The golden ratio also appears in many polygons and polyhedrons of interest not just to mathematicians but to artists, architects, and even botanists, as it appears in the spacing of leaves around the stems of many plants. But interest in the ratio has spurred no end of specious or outright fictitious claims about its appearance, including an oft-repeated one about its inclusion in the dimensions of the Parthenon (obtained by gaming the measurements to achieve the desired result) and another claiming Leonardo da Vinci used it in the Mona Lisa (similarly bogus). Livio devotes so much of the book to debunking these and other claims that by the time he gets around to discussing the golden ratio’s actual appearances in art, architecture, and nature, he’s devalued his subject by spending too little time explaining where φ is and too much time explaining where it ain’t.

Next up: I’m a bit behind here, having already finished Michael Ruhlman’s superb The Making of a Chef: Mastering Heat at the Culinary Institute of America, the book that first established him as one of the best writers on food and cooking today.

Filed Under: Uncategorized Tagged With: , , ,
→ March 31, 2012
→ By

Saturday five, #2.

Five books, five links to my own stuff, and five links to others’ articles.

I’ve read eight books since my last post on any of them, so I’m going to take a shortcut and catch up by highlighting the five most interesting. Now that spring training is ending, I hope to get back to regular dishblogging soon.

* Charles Seife’s Zero: The Biography of a Dangerous Idea is the one non-fiction book in this bunch, a history-of-math tome that incorporates a fair amount of philosophy, physics, and religion all in a book that’s under 200 pages and incredibly readable for anyone who’s at least taken high school math. The subject is the number zero, long scorned by philosophers, theologians, and even some mathematicians who resisted the idea of nothing or the void, yet which turned out to be critical in a long list of major scientific advances, including calculus and quantum mechanics. I generally prefer narrative non-fiction, but Zero moves as easily as a math-oriented book can get without that central thread.

* Dashiell Hammett’s Nightmare Town is one of three major Hammett short-story collections in print (along with The Continental Op and the uneven The Big Knockover), and my favorite for its range of subjects and characters without feeling as pulpy as some of his most commercial stories. The twenty stories are all detective stories of one sort or another starring several different Hammett detectives, including early iterations of Sam Spade and the character who eventually became the Thin Man, as well as a western crime story that might be my favorite short piece by Hammett, “The Man Who Killed Dan Odams.”

* Readers have recommended Tim O’Brien’s short story cycle The Things They Carried for several years, usually any time I mention reading another book that deals with the Vietnam War and/or its aftermath. The book, a set of interconnected stories that feels like an novel despite the lack of a central plot, is based heavily on O’Brien’s own experiences in that conflict, especially around death – of platoon mates, of Viet Cong soldiers, of Vietnamese civilians, and of a childhood crush of O’Brien’s who died at age 9 of a brain tumor. The writing is remarkable, more than the stories themselves, which seemed to cover familiar ground in the genre, as well as O’Brien’s ability to weave all of these disconnected stories into one tapestry around that central theme of death and the pointlessness of war. The final story, where he ties much of it together by revisiting one of the first deaths he discussed in the book, is incredibly affecting on two levels as a result of everything that’s come before.

* I’m a big Haruki Murakami fan – and no, I haven’t read 1Q84 yet and won’t until it’s in paperback – but Dance, Dance, Dance was mostly a disappointment despite some superficial entertainment value, enough to at least make it a quick read if not an especially deep one. A sequel of sorts to A Wild Sheep Chase, it attempts to be more expansive than that earlier novel but still feels like unformed Murakami, another look at him as he built up to The Wind-Up Bird Chronicle, a top-ten novel for me that hit on every level. Dance is just too introspective, without enough of Murakami’s sort of magical realism (and little foundation for what magical realism it does contain) and no connection between the reader and the main character.

* I loved Edith Wharton’s The Age of Innocence, a funny, biting satire on upper-class life in the United States just after World War I, so I looked forward to House of Mirth, present on the Modern Library and Bloomsbury 100 lists, expecting more of that sharp wit but receiving, instead, a dry, depressing look at the limitations of life for women in those same social circles prior to the war. It’s a tragedy with an ironic title that follows Lily Bart through her fall from social grace, thanks mostly to the spiteful actions of other women in their closed New York society; it’s a protest novel, and one of the earliest feminist novels I’ve read (preceded, and perhaps inspired, by Kate Chopin’s The Awakening), but I found myself feeling more pity than empathy for Lily as a victim of circumstances, not of her own missteps.

Next up: I’m reading Martin Booth’s A Very Private Gentleman (filmed as The American) and listening to Jonah Lehrer’s Imagine: How Creativity Works. The Booth book is on sale through that link for $5.60.

–

Five things I wrote or said this week:

On Jeff Samardzija’s revival.

This week’s chat.

One batch of spring training minor league notes, including the Angels, A’s, Rangers, and Royals.

Tuesday’s “top 10 players for 2017” column, which I emphasized was just for fun and still got people far too riled up. There’s no rational way to predict who the top ten players will be in five years and I won’t pretend I got them right. But it was fun to do.

I interviewed Top Chef winner and sports nut Richard Blais on the Tuesday Baseball Today podcast, in which he talked about what it was like to “choke” (his word) in the finals on his first season and then face the same situation in his second go-round. We also talked about why I should break my ten-year boycott of hot dogs.

—

And the links…

* The best patent rejection ever, featuring Borat’s, er, swimsuit.

* A spotlight on Massachusetts’ outdated liquor laws. For a state that likes to pretend it’s all progressive, Massachusetts is about thirty years behind the times when it comes to alcohol, to say nothing of how the state’s wholesalers control the trade as tightly as the state liquor board does in Pennsylvania. The bill this editorial discusses would be a small start in breaking apart their oligopoly, but perhaps enough to start to crumble that wall.

* I admit it, I’m linking to Bleacher Report, but Dan Levy’s commentary on how Twitter has affected what a “scoop” means, especially to those of us in the business, is a must read. And there’s no slidshow involved.

* The Glendale mayor who drove the city into a nine-figure debt hole by spending government money to build facilities for private businesses – including the soon-to-be-ex-Phoenix Coyotes – won’t run for a sixth term, yet she’s receiving more accolades than criticism on the way out. Put it this way: Given its schools, safety, and public finances, we never considered Glendale for a second when looking to move out here.

* The “pink slime” controversy has led the manufacturer to suspend production at three of its four plants. That makes for a good headline, but are job losses really relevant to what should be a discussion of whether this is something people, especially schoolchildren, should be consuming? And now the controversy is moving on to carmine dye, derived from an acid extracted from cochineal beetles and used in Starbucks frappuccinos. If nothing else, I applaud the new emphasis on knowing exactly what we’re eating.

Filed Under: Uncategorized Tagged With: , , , , , , , , , , ,