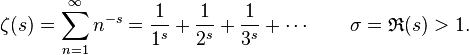For Insiders this week, I wrote four pieces. I broke down the Astros’ trade for Justin Verlander and the Angels’ trade for Justin Upton. I put up scouting notes on prospects from the Yankees, Phillies, Jays, and Rangers. And I looked at five potential prospect callups for September. I also held a Klawchat on Thursday.
At Vulture this week, I looked at five major Game of Thrones-themed boardgames, not just reskinned games but several original titles like the excellent GoT Card Game. For Paste, I reviewed the Tour de France-themed boardgame La Flamme Rouge, which is light and good for family play. And here on the dish I reviewed the strong app version of the two-player game Jaipur, a steal at $5.
I’m trying something new this week, and if you find it useful I’d appreciate your feedback. I get a lot of press releases on boardgames from publishers, so I’m including the best of those at the end of this run of links along with boardgame-related news items. These will include Kickstarter announcements that look interesting to me, and if I’ve seen a game at all I’ll indicate it in the blurb.
This is your regular reminder that my book Smart Baseball is available everywhere now in hardcover, e-book, and audiobook formats. Also, please sign up for my free email newsletter, as my subscriber count is down one after I removed that one guy who complained about the most recent edition and called me a “tool.”
And now, the links…
- Longread of the week: GQ sent essayist Rachel Kaadsi Ghansah to South Carolina to look for answers in the background of mass murderer Dylan Roof, although I don’t know that she found any. This was a severely mentally ill man with a criminal background who was allowed to purchase a gun.
- Another longread from Lapham’s Quarterly, published a few years ago: On the brief career and unsolved disappearance of Barbara Follett, a child novelist who published two novels and wrote two more before her still-mysterious vanishing at age 25.
- A German mathematician claimed he has solved the P vs. NP problem, and done so with the negative (but most likely correct) answer that P does not equal NP – that is, that there are some computational problems (NP) that cannot be reduced to equivalence with other problems (P) that we know can be solved in polynomial time. Norbert Blum has since posted a comment on the proof’s page saying “The proof is wrong,”, so perhaps we’re still not there yet.
- The planet is warming, including the oceans, and that latter temperature increase could lead to much smaller fish.
- Consumers are increasingly demanding antibiotic-free meat, including chicken, but can chicken producers “afford” to make the switch? Of course they can, and maybe meat will cost more in the end, but the cost of doing nothing – of continuing prophylactic use of antibiotics and dealing with the multi-drug resistant bacteria that will result – is far greater.
- Eight of the 28 members of a DHS advisory panel on cybersecurity quit en masse last week, arguing that the President is ignoring threats to critical infrastructure.
- Meanwhile, Trump continues to fill the swamp with political appointees, often taking people from industry and putting them in regulatory positions overseeing those businesses, as ProPublica continues to investigate these unreported hirings.
- Presidential adviser (and son-in-law) Jared Kushner is hundreds of millions of dollars in debt to foreign investors on a building he sort-of owns in Manhattan. Bloomberg investigates Kushner & associates’ attempts to solicit new investments from foreign sources as well as the troubled finances of his real estate firm.
- A reader passed along this 2007 study of New Orleans residents who chose not to evacuate before Hurricane Katrina hit, looking at reasons why they didn’t leave. The “Perceived Barriers to Action” section of the conclusions is the money part – literally, as financial barriers were a significant issue.
- Jay Caspian King looks at why some new sports stats catch on and others don’t for the NY Times. I think he undersells the point in his last paragraph about our obsession with round numbers, though.
- One of my colleagues, Ed Cunningham, walked away from his job as a football announcer because he was concerned about the impact of brain injuries in the sport.
- Awful Announcing looks at Joe Sheehan and his subscription-only newsletter, and how he’s managed to make a living charging for content in an era where free content was still king. Disclaimer: Joe’s a good friend of mine dating back to the early days of Baseball Prospectus.
- A Yemeni social media star who’d reported on and criticized both sides in that country’s devastating civil war has been abducted by Houthi rebels, the forces loyal to Yemen’s deposed dictator. The civil war has led to countless deaths and a cholera epidemic.
- Parents of autistic children have become targets for a host of unproven or dangerous “treatments” for the genetic condition, a situation exacerbated by what the writer calls “online filter bubbles” of shared junk science stories.
- The University of Tampa fired a professor who suggested Hurricane Harvey was karma for Texas Republicans. I can’t blame them – it was stupid, insensitive, and obviously false. You can have those thoughts, you may even be entitled to share them in your classroom, but once you put that on social media for the world to see, you’ve changed the stakes.
- Speaking of Harvey, the Washington Post asked Texas Republicans who voted against aid for victims of the ‘superstorm’ Sandy in 2013 to defend their votes; only one answered, and he did so with a lie about the Sandy bill. The Republicans also failed to answer the Post‘s questions about Harvey and climate change.
- Trevor Noah offered a ridiculous, specious criticism of the “antifa” movement in what seemed to me like some sort of weak-ass attempt to satisfy a fairness doctrine. In fact, law enforcement authorities, including the FBI and CIA, appear to place the blame for so-called “antifa” attacks on Trump himself, due to the “inflammatory rhetoric and policies” he’s espoused as candidate and now president.
- A size-10 model has returned her beauty pageant crown after the event organizers told her to lose weight. There are several pictures of the woman in the article, and if that woman needs to shed some pounds, then I’d say 99% of the planet is obese.
- A first-time author appears to have gamed the NYT Bestseller list largely through bulk sales of her own book. The author, Lani Sarem, has denied any shenanigans. I found it surprising that the Times‘ bestseller lists are still assembled in such an ad hoc fashion more than 20 years after the music industry went to hard sales data collected by SoundScan.
- The Guardian asked three authors to discuss their favorite Philip K. Dick novels ahead of this fall’s release of a sequel to Blade Runner, which was based on Dick’s novel Do Androids Dream of Electric Sheep? I was surprised none of them discussed The Man in the High Castle, my favorite PKD novel and his lone book to win the Hugo Award.
- The Guardian also ran an op ed this week arguing that Google, Facebook, and amazon should be “nationalized” because of their quasi-monopoly status. This is a pretty terrible idea across the board.
- But it does appear that Google dropped the hammer on a think tank it supports, leading it to fire several of its experts, as one of the deposed academics writes in the Washington Post. This seems to go against Google’s “don’t be evil” policy.
- The NY Times ran a quirky op ed this week in praise of memorizing poems. This used to be common practice, and it’s evident if you read novels from across the last 150 years or so that the practice has gone away, as quotes and allusions to classical poetry have declined.
- Also from the Grey Lady, editorial writer Bret Stephens shared fifteen tips for aspiring op ed writers – but most of these are just good tips for writers, period.
- I’ve never tried the video game franchise Overwatch in part because I hear it’s a lot of first-person shooting, and Paste opines that it’s time for the designers to give players something else to do. I never cared for the earliest generation of FPS games, like Castle Wolfenstein or Doom, and that’s around the time I started to fade out of video gaming.
- Boardgame news: Kotaku looks deeper at Photosynthesis, one of the biggest buzz games at GenCon this year. I ranked Photosynthesis seventh on my list of the best new games at GenCon.
- Playing boardgames with other people can make you a nicer person with better relationships.
- There’s a new virtual reality version of Catan coming out for the holidays. I’m really not sure what the market for this is; how will VR add to the Catan gaming experience?
- Plan B Games, founded by former Z-Man owner/head Sophie Gravel, announced Azul, an upcoming game with a Moorish theme and artwork, due out in October. They didn’t have this out at GenCon, so it’s new to me as well.
- Greenbrier Games has reopened its Kickstarter for the fantasy/adventure boardgame Champions of Hara, which will also include some miniatures and upgraded artwork.
- Greater than Games announced a Legends of Sleepy Hollow boardgame (PDF link), with a Kickstarter beginning on October 17th.