Prime Obsession.

I admit it: I am not afraid of math.

And if you’re not afraid of math either – in this case, some fairly heavy math – you might enjoy Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics as much as I did. It’s a book about an obscure question in the field of number theory, one that remains unsolved after 150 years and probably has little to no practical application, but John Derbyshire manages to give the subject some real personality while doing his best to make it accessible to readers who haven’t taken a lot of advanced math classes or who, like me, are a good 13 years removed from their last one.

The subject of Prime Obsession is the Riemann Hypothesis, which states that the non-trivial zeros of Riemann’s zeta function are half part real. “Non-trivial zeros,” in this case at least, are complex numbers (a + bi, where i is the imaginary number defined as the square root of negative 1 and b is nonzero) that give the result of 0 when plugged into the zeta function. “Half part real” means that a in that complex number is equal to ½.

The zeta function is the crux of the matter, the sum of the following infinite series:

That is:

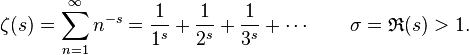
Riemann posed his hypothesis when studying the Prime Number Theorem, which states that for any random number N, the probability of N being prime (and thus the frequency of primes around N) is roughly equal to the reciprocal of the natural logarithm of N, that is, 1/ln(N). In his one paper on the subject, he hypothesized that the frequency of primes and the differences between the actual frequency and the predicted frequency in the Prime Number Theorem was connected to the zeros of this zeta function. He couldn’t prove it at the time, and even though David Hilbert declared it one of the great mathematical problems of the 20th century in 1900, one of a list that has seen all but two of its number* solved, and in 2000 the Riemann Hypothesis was named one of the Millennium Prize Problems by the Clay Mathematics Institute, it remains unsolved. Prove or disprove it and you’ll get a cool million bucks for your trouble.

As you might imagine, solving the problem isn’t easy; indeed, it stands unsolved more than a decade after Sir Andrew Wiles’ solution of the equally perplexing problem of Fermat’s Last Theorem, one that required the development of an entire new field of mathematics (topology) unknown to Fermat at the time that he wrote that he had a “truly marvelous proof” to the problem. (Current thought is that whatever proof he had was incomplete.) The difficulty of proving or disproving the Riemann Hypothesis has led many of the major figures in mathematics, particularly in number theory, to attempt to tackle all or part of the problem or to work on further theorems and conjectures that build on the assumption that the “RH” is true. (And it has at least held true so far for very large numbers, which is not a proof but is weak evidence in its favor.)

Derbyshire’s main difficulty, beyond the lack of a clear resolution to the story, is making the solution of a potentially useless mathematical conundrum interesting; Wiles’ proof of Fermat’s Last Theorem was momentous and newsworthy, but the practical applications have been nil – it’s merely interesting to people who like numbers. Proving the Riemann Hypothesis would likely have a similar lack of real-world effects, and the hypothesis itself is a lot harder to grasp than Fermat’s Last Theorem was; the latter problem had an incredibly complex solution, but the question itself was easy for anyone who’d taken algebra to understand. Derbyshire does a masterful job of walking through the history of the Riemann Hypothesis, from earlier work on prime numbers, including the PNT, through Riemann’s brief life and career in mathematics to the major developments in the 151 years since his seminal paper appeared.

The book alternates between chapters walking through the math and chapters on the history and personalities involved in the hypothesis’ history. Carl Friedrich Gauss has a starring role early, while G.H. Hardy, Leonhard Euler, J.E. Littlewood, Jacques Hadamard, and Hilbert appear at some length later on. Derbyshire sprinkles stories of their peculiarities, senses of humor, and non-mathematical interests to keep the text lighter while also highlighting the chance occurrences that made some of the progress on the proof possible and regularly pointing out the remarkable longevity of most of the major mathematicians he mentions.

His math writing, while clearly geared to a lay audience, still got fuzzy for me when he got deeper into the zeta function as he tried to map it to the complex plane. Derbyshire relies on these “visual” interpretations that don’t correspond to any sort of plane or graphs that I’ve seen elsewhere, and I felt it was the one time he presupposed some familiarity with higher math on the part of the reader. But to his credit, he relies largely on algebra and gives a brief (re-)introduction to differentiation and integration for the short periods where calculus is necessary to move the math story forward. He also hits many major touchstones that will unlock memories for those of you who took and enjoyed lots of math classes, from the Sieve of Eratosthenes to the amazing Euler’s Identity, the latter of which states that

And if you look at that formula and are amused, fascinated, or just generally intrigued, Prime Obsession is a book for you.

I also recommend a book about one of the mathematicians who makes a cameo appearance in Derbyshire’s book, The Man Who Loved Only Numbers: The Story of Paul Erd?s and the Search for Mathematical Truth. Erd?s was a Hungarian-born savant who lived most of his life out of a suitcase, traveling the world, arriving at the doors of mathematicians he knew and announcing that “my brain is open,” after which he’d settle in for a few days or weeks and embark with his host on a streak of problem-solving and paper-writing. He had his own peculiar vocabulary, consumed large quantities of caffeine and later amphetamines, and combined brilliance and prolificacy (that’s peak and longevity for you Hall of Fame watchers) to the point where other mathematicians are referred to by their “Erd?s number,” where a person who co-authored a paper with Erd?s has an Erd?s number of one, while others are marked by how many papers you must go through to create the shortest possible chain back to Erd?s.